Mocha and Diana

time limit per test: 2 seconds

memory limit per test: 256 megabytes

Articles

This is the hard version of the problem. The only difference between the two versions is the constraint on $n$. You can make hacks only if all versions of the problem are solved.

A forest is an undirected graph without cycles (not necessarily connected).

Mocha and Diana are friends in Zhijiang, both of them have a forest with nodes numbered from $1$ to $n$, and they would like to add edges to their forests such that:

• After adding edges, both of their graphs are still forests.
• They add the same edges. That is, if an edge $(u,v)$ is added to Mocha’s forest, then an edge $(u,v)$ is added to Diana’s forest, and vice versa.

Mocha and Diana want to know the maximum number of edges they can add, and which edges to add.

Input

The first line contains three integers $n$, $m1$ and $m2\ (1≤n≤10^5, 0≤m1,m2<n)$ — the number of nodes and the number of initial edges in Mocha’s forest and Diana’s forest.

Each of the next $m1$ lines contains two integers $u$ and $v\ (1≤u,v≤n, u≠v)$ — the edges in Mocha’s forest.

Each of the next $m2$ lines contains two integers $u$ and $v$ $(1≤u,v≤n, u≠v)$ — the edges in Diana’s forest.

Output

The first line contains only one integer h, the maximum number of edges Mocha and Diana can add.

Each of the next $h$ lines contains two integers $u$ and $v$ $(1≤u,v≤n, u≠v)$ — the edge you add each time.

If there are multiple correct answers, you can print any one of them.

Examples

input

3 2 2
1 2
2 3
1 2
1 3

output

0

input

5 3 2
5 4
2 1
4 3
4 3
1 4

output

1
2 4

input

8 1 2
1 7
2 6
1 5

output

5
5 2
2 3
3 4
4 7
6 8

Note

In the first example, we cannot add any edge.

In the second example, the initial forests are as follows.

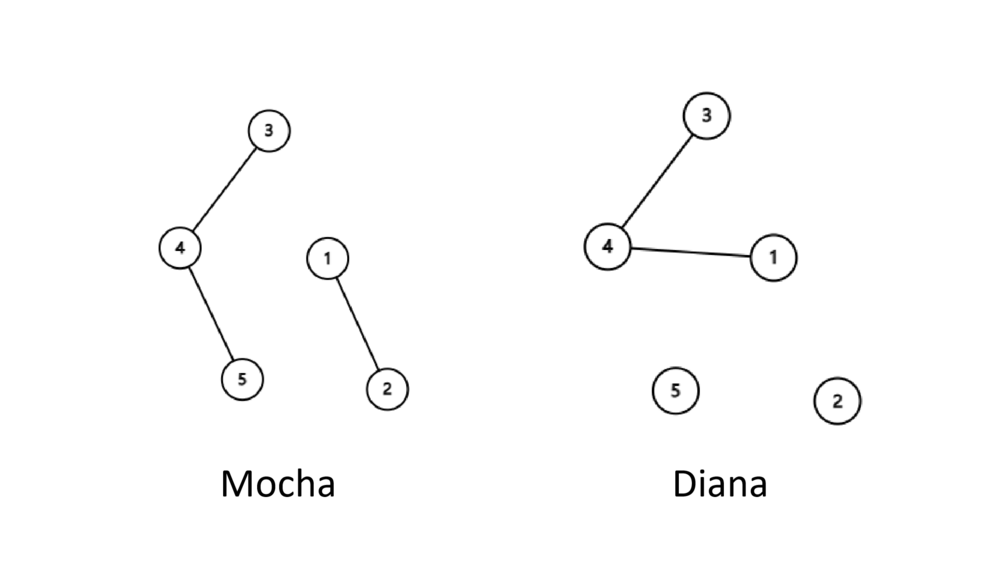
We can add an edge $(2,4)$.

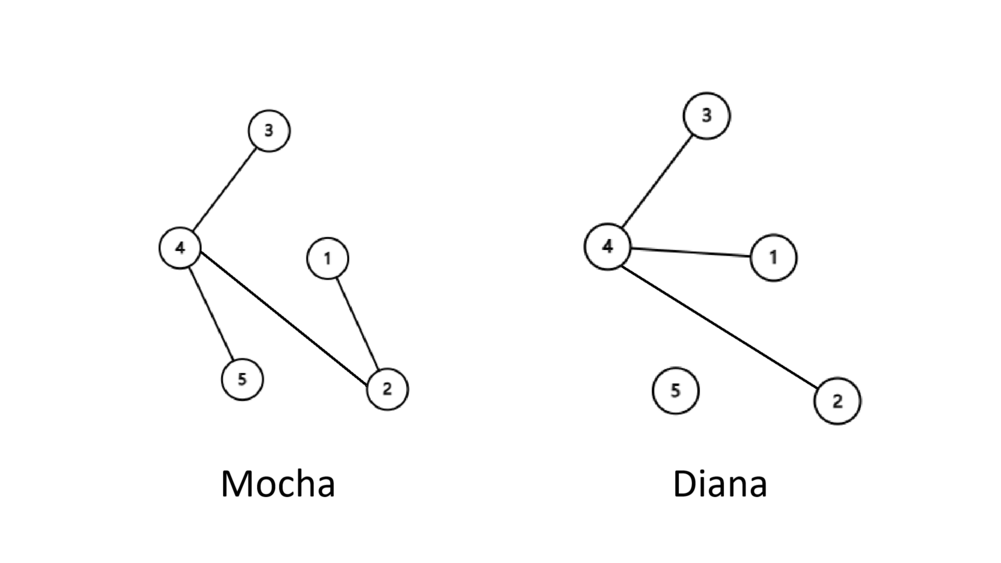
Tutorial

找到在第一个森里中不与 $1$ 连通，且在第二个森林中也不与 $1$ 连通的点，与 $1$ 相连。

重复上述操作直到没有点符合要求。

在新得到的两个森林中，所有的点要么与第一个森林的 $1$ 连通，要么与第二个森林的 $1$ 连通（与两个森林的 $1$ 都连通的点除外）。

而上述两种点可以相互匹配加边，直到某个森林变成树为止。

Code

#include<bits/stdc++.h>

using namespace std;

const int maxn = 1e6+1;
int f1[maxn], f2[maxn];
int a[maxn], b[maxn];

int fd1(int x) {
    if (f1[x] == x) return x;
    return f1[x] = fd1(f1[x]);
}

int fd2(int x) {
    if (f2[x] == x) return x;
    return f2[x] = fd2(f2[x]);
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n, m1, m2;
    cin >> n >> m1 >> m2;
    for(int i = 1; i <= n; ++ i) {
        f1[i] = f2[i] = i;
    }
    for(int i = 1; i <= m1; ++ i) {
        int u, v;
        cin >> u >> v;
        int x = fd1(u), y = fd1(v);
        f1[x] = y;
    }
    for(int i = 1; i <= m2; ++ i) {
        int u, v;
        cin >> u >> v;
        int x = fd2(u), y = fd2(v);
        f2[x] = y;
    }
    long long x1 = fd1(1), y1 = fd2(1), tot = 0;
    for(int i = 1; i <= n; ++ i) {
        int x = fd1(i), y = fd2(i);
        if (x1 != x && y1 != y) {
            f1[x] = x1, f2[y] = y1;
            ++tot; a[tot] = 1, b[tot] = i;
        }
    }
    for(int i = 1, j = 1; i <= n; ++ i) {
        if (fd1(i) == x1) continue;
        while(j <= n && fd2(j) == y1) j ++;
        if (j == n+1) break;
        int x = fd1(i), y = fd2(j);
        ++tot; a[tot] = x, b[tot] = y;
        f1[x] = x1, f2[y] = y1;
    }
    cout << tot << "\n";
    for(int i = 1; i <= tot; ++ i) {
        cout << a[i] << " " << b[i] << "\n";
    }
    return 0;
}